Wishing you a Happy New Year 2023
We are just a few more hours away from entering into 2023. The celebrations on the New Year’s Eve were kind of muted on last two occasions due to global pandemic, but this year people are about to go off with a bang with fireworks, as there are no more covid restrictions.
Regardless of how you choose to celebrate, the New Year’s Eve is a perfect time to reflect on the past year and look forward to the new possibilities and opportunities that the future holds. It’s natural to feel curious about how the new year will unfold and to wonder what tomorrow will bring.
While it’s certainly difficult to predict the future or foretell future events, we can always take solace in Math to find what 2023 will bring for us. So, let’s start with some fun facts.
2023 is a Harshad number
Harshad numbers were discovered by one of my favorite recreational mathematician D. R. Kaprekar (I’ve already written about his other discovery of Kaprekar constant 6174 here). Harshad numbers are integers that are divisible by the sum of their digits.
For example, the number 18 is a Harshad number because it is divisible by the sum of its digits (1 + 8 = 9, and 18 is divisible by 9). Another example is 12, (1 + 2 = 3, and 12 is divisible by 3). Kaprekar named these numbers as Harshad, meaning giving joy (Sanskrit harsha, joy + da taddhita pratyaya, causative).
So, let’s find out if the year 2023 is Harshad or not by writing few lines of code in Mathematica [You can try these commands on a free version of Mathematica that comes with every Raspberry Pi or you can always follow up online in Wolfram Cloud].
harshadQ[h_Integer] := Divisible[h, Total[IntegerDigits[h]] harshadQ[2023] True
So, 2023 will be full of joy and happiness as it is a Harshad number :)
Now, let’s try to visualize these Harshad numbers. One of my favorite ways is to take first 10,000 numbers, arrange them in 100x100 grid, if the number is Harshad, we will color it with green, and if otherwise, then blue.
ArrayPlot[Partition[Range[10000], 100] ColorFunction -> (If[harshadQ[#], Green, Blue] &), ColorFunctionScaling -> False, ImageSize -> 800, Mesh -> True, MeshStyle -> Black, DataReversed -> True, Frame -> True, FrameTicks -> All, FrameTicksStyle -> Directive[Black, 14]]
Harshad numbers: 10,000 numbers arranged in a 100x100 grid and Harshad numbers are coloured green
Let’s try with one million digits to check if there are any patterns to understand how Harshad numbers are distributed.
ArrayPlot[Partition[Range[10^6], 1000] ColorFunction -> (If[harshadQ[#], Blue, White] &), ColorFunctionScaling -> False, ImageSize -> 800, Mesh -> None, MeshStyle -> Black, DataReversed -> True, Frame -> True, FrameTicks -> All, FrameTicksStyle -> Directive[Black, 14]]
1000,000 numbers arranged in a 1000x1000 grid and Harshad numbers are colored blue
2023 is a Lucky number
In number theory, a lucky number is a natural number in a set, generated by a sieving process, which is similar to the Sieve of Eratosthenes that generates the primes numbers. Here are the steps for the lucky number sieve:
Start with a list of all positive integers from 1 to a chosen number (e.g., 1 to 100).
Eliminate all numbers that contain the digit 2 or are divisible by 2.
The first number remaining in the list after 1 is 3, so every third number (beginning at 1) is eliminated.
The next surviving number is now 7, so every seventh remaining number is eliminated.
Repeat the process for any other digits or numbers that are considered unlucky or undesirable.
The remaining numbers are considered to be lucky numbers.
Let’s write the code:
luckyNumbers[n_Integer] := Module[{i = 1}, Catch[NestWhile[(i+
If[Length[#1] > i,
Delete[#1, List /@ Range[#1[[i]], Length[#1], #1[[i]]]],
Throw[#1]]) &, Range[1, n, 2], UnsameQ, 2]]];
luckyNumbers[2025]
{1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99, 105, 111, 115, 127, 129, 133, 135, 141, 151, 159, 163, 169, 171, 189, 193, 195, 201, 205, 211, 219, 223, 231, 235, 237, 241, 259, 261, 267, 273, 283, 285, 289, 297, 303, 307, 319, 321, 327, 331, 339, 349, 357, 361, 367, 385, 391, 393, 399, 409, 415, 421, 427, 429, 433, 451, 463, 475, 477, 483, 487, 489, 495, 511, 517, 519, 529, 535, 537, 541, 553, 559, 577, 579, 583, 591, 601, 613, 615, 619, 621, 631, 639, 643, 645, 651, 655, 673, 679, 685, 693, 699, 717, 723, 727, 729, 735, 739, 741, 745, 769, 777, 781, 787, 801, 805, 819, 823, 831, 841, 855, 867, 873, 883, 885, 895, 897, 903, 925, 927, 931, 933, 937, 957, 961, 975, 979, 981, 991, 993, 997, 1009, 1011, 1021, 1023, 1029, 1039, 1041, 1053, 1057, 1087, 1093, 1095, 1101, 1105, 1107, 1117, 1123, 1147, 1155, 1167, 1179, 1183, 1189, 1197, 1201, 1203, 1209, 1219, 1231, 1233, 1245, 1249, 1251, 1261, 1263, 1275, 1281, 1285, 1291, 1303, 1309, 1323, 1329, 1339, 1357, 1365, 1369, 1387, 1389, 1395, 1401, 1417, 1419, 1435, 1441, 1455, 1459, 1471, 1473, 1485, 1491, 1495, 1497, 1501, 1503, 1519, 1533, 1543, 1545, 1563, 1567, 1575, 1579, 1585, 1587, 1597, 1599, 1611, 1639, 1641, 1645, 1659, 1663, 1675, 1693, 1701, 1705, 1711, 1723, 1731, 1737, 1749, 1765, 1767, 1771, 1773, 1777, 1797, 1801, 1809, 1819, 1827, 1831, 1833, 1839, 1857, 1869, 1879, 1893, 1899, 1915, 1921, 1923, 1933, 1941, 1945, 1959, 1963, 1965, 1977, 1983, 1987, 1995, 2001, 2019, 2023}So, 2023 year will certainly will bring luck to all of you :)
Let’s visualize first 3000 lucky numbers by arranging them in 30x100 grid and coloring them with green.
ArrayPlot[Partition[Range[3000], 100], ImageSize -> 800
ColorRules ->
Append[Thread[
luckyNumbers[3000] ->
Green] /. {2023 -> Green} :> {2023 -> Red}, _ -> Blue],
DataReversed -> True, Mesh -> True, MeshStyle -> Gray, Frame -> True,
FrameTicks -> {{Range[0, 30, 1], None}, {Range[0, 100, 5], None}},
FrameTicksStyle -> Directive[Black, 14], AspectRatio -> 1/1.5]3000 numbers are arranged in 30x100 grid and lucky numbers are coloured green
2023 is a Polite number
In number theory, a number is called Polite if it can be written as the sum of at least two consecutive natural numbers.
For example, 12 = 3 + 4 + 5
Another example, 7 = 3 + 4
For 2023,
2023 = 111 + 112 + 113 + 114 + 115 + 116 + 117 + 118 + 119 + 120 + 121 + 122 + 123 + 124 + 125 + 126 +127
The year 2023 is asking us to be polite :)
We encourage our readers to write a program to establish if the number is polite or impolite. Keep an eye over the future articles where we go in depth about numbers.
Finding 2023 in e, Pi, and Golden Ratio
We know that Pi is an irrational number- i.e., it can’t be expressed as a ratio of two integers; and contains an infinite number of digits. Moreover, these digits have no apparent pattern or in other words they are randomly distributed. Now can we locate a specific pattern or finite sequence of digits such as 2023 in these randomly behaving digits of Pi or in other famous irrational numbers such as Euler number [e] and Golden Ratio [Phi].
Harold Finch in “Person of Interest” (one of favorite serial) has explained beautifully here-
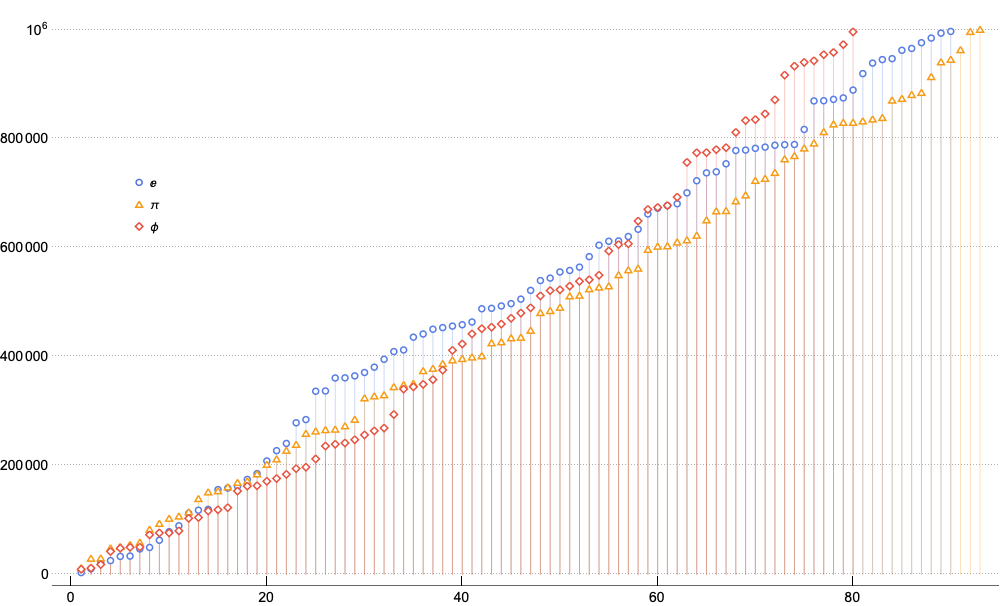
Since we are already in the year 2023, let us try to find the occurrence of number 2023 in the decimal expressions of e, Pi, and Phi [up to 1 million digits].
ListPlot[Flatten
Position[
Partition[First[RealDigits[N[#, 10^6]]], 4, 1],
{2, 0, 2, 3}]] & /@ {E, Pi, GoldenRatio},
PlotTheme -> "Business",
ImageSize -> 1000,
PlotLegends -> Placed[{E, Pi, GoldenRatio}, Scaled[{0.1, 0.65}]],
PlotMarkers -> {"OpenMarkers", Medium}, Filling -> Bottom,
FrameTicksStyle -> Directive[Black, 14]]Finding occurrence of 2023 in the of digits e, Pi, and Golden Ratio
And here we end our musings on the number 2023. You can check other neat ways to compute the number 2023 in this recent reddit thread.
If you wish to learn more about such numbers in-depth, stay tuned for the announcement of our Computational Learning Platform.
I hope that the new year brings you joy, happiness, and success, and that you are able to accomplish all of your goals and aspirations.
































![Frequency of Kaprekar sequence for four digit numbers [in base 10]. The numbers at the left denotes the number of steps required to reach the Kaprekar constant.](https://images.squarespace-cdn.com/content/v1/5194b056e4b0acc777d71b74/1398789067287-EPNZNMWS442SADSMXVE8/Frequency+of+Kaprekar+sequence++for+four+digit+numbers+%5Bin+base+10%5D.)







